Gustav Robert Kirchhoff's Current Law
A node is a point in the circuit where components are connected together. We can think of the precise point as the solder connection, but the node actually includes all the wires and component leads connected to that point, because they are all at the same voltage. (This assumes that wires are perfect conductors, which is a reasonable assumption in most situations.) Consider, for example, the Ampeg B-22-X high-gain input circuit.
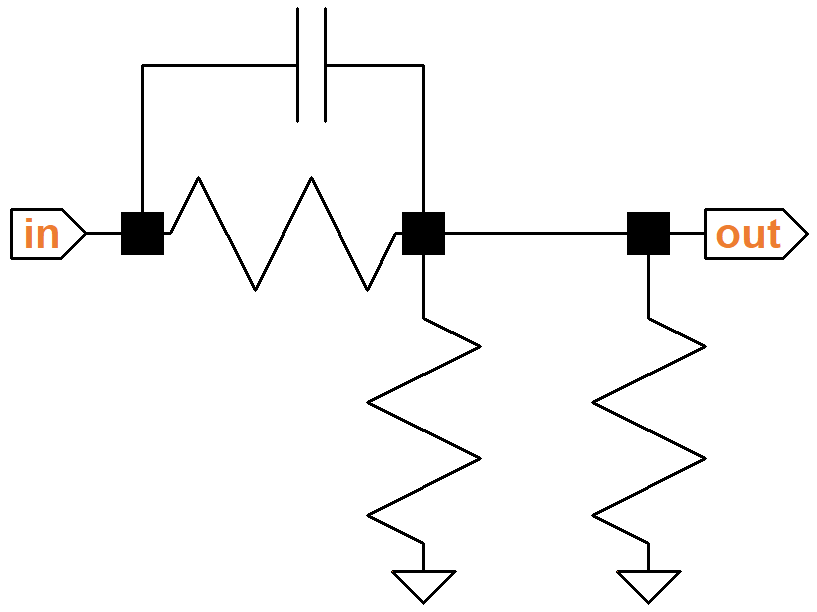
There are three nodes in this circuit: in, out, and ground.
Kirchhoff's Current Law
According to Kirchhoff's Current Law, or KCL as it is known, the sum of the currents entering a node equals the sum of the currents leaving a node.
Problem
Consider the screen supply of the Fender Bassman 5F6-A. At idle, the total current load of the power tube screens, the phase inverter, and the preamps is 11mA. This current is supplied via the choke, which smoothes out ripples in the flow. Suddenly we hit our power chord and bring the amp instantly to full power, where the screen current increases substantially, raising the total current load from 11mA to 27mA. After a few tenths of a second the current through the choke rises to 27mA, but initially all of the extra current is supplied by the capacitor. What is this initial current IC?
Solution
The unknown current IC and 11mA are entering the node in the upper right and 27mA is leaving it. According to Kirchhoff's Current Law
IC + 11mA = 27mA
Thus
IC = 16mA
KCL in Practice
Kirchhoff's Current Law allows us to determine an unknown current based on known currents. To be honest, his voltage law is more important to tube amps. The nuances of power supply sag and some power tube calculations are notable exceptions.
