Imaginary Numbers

The measurable tonal improvement you can achieve by shifting from solid to stranded wire, the signing bonus you'll get if you convert your amp from fixed to cathode bias, the profit you can make writing books about guitar amplifier circuit design - these are just a few examples of imaginary numbers in our daily lives.

If tube amps only used resistors, if there were no capacitors or inductors, if there were no parasitic capacitances or inductances, then there would be no need for knowing complex algebra, the mathematics that handles imaginary numbers. As intimidating as it sounds, complex algebra is merely an extension of high school algebra - no knowledge of calculus is required. Yet it is an extremely powerful tool to a circuit designer, because Ohm's Law and Kirchoff's Laws apply to any combination of resistors, capacitors, and inductors when they are represented as "complex" impedances.

Common Algebra

Complex algebra is an extension of a first-year algebra course in high school, what mathematicians call "common algebra" and 9th graders call "unusual punishment." Consider some of these aspects of common algebra:

100+50 = 50+100 = 150 (for addition, order doesn't matter)

100-50 = 50, whereas 50-100 = -50 (for subtraction, order matters)

100-50 = 100+(-50) = 50 (subtraction is the same as adding a negative number)

(100)(5) = (5)(100) = 500 (for multiplication, order doesn't matter)

100/50 = 2, whereas 50/100 = 0.5 (for division, order matters)

100/50 = 100(1/50) = 2 (division is the same as multiplying by the reciprocal)

Does this look familiar? Complex algebra, for what we need as tube amp designers, is not much of a leap from here.

New! Guitar Amplifier Electronics: Fender Deluxe - from TV front to narrow panel to brownface to blackface Reverb

Complex Algebra

Common algebra uses real numbers. Complex algebra introduces the concept of "imaginary" numbers. Historically this strange name resulted from a need to describe the square root of a negative number. For example, because (2)(2) = 4, we say that the square root of 4 is 2. In other words, the number 2 multiplied by itself equals 4, therefore the square root of 4 is 2. The square root of -4 does not exist, because no real number multiplied by itself equals -4.

Let's "imagine" that such a number does exist. We'll designate it as being imaginary by putting the symbol j in front of it. (Mathematicians and physicists like to use i but circuit designers reserve this letter for current.) So we imagine there exists an imaginary number j2 such that

(j2)(j2) = -4

Here are some examples of complex algebra. You don't need to memorize these rules because in a moment I'll describe one simple rule to keep it all straight.

The addition and subtraction of imaginary numbers is similar to what we learned for real numbers:

j100+j50 = j50+j100 = j150

j100-j50 = j50

j50-j100 = -j50

j100-j50 = j100+(-j50) = j50

Guitar Amplifier Electronics: Basic Theory - master the basics of preamp, power amp, and power supply design.

The multiplication of two imaginary numbers results in a real number, but is the negative of what would result if the numbers were real:

(j100)(j5) = (j5)(j100) = -500

(j100)(-j5) = (-j100)(j5) = 500

The multiplication of a real number and an imaginary number results in an imaginary number:

(j100)(5) = j500

The division of an imaginary number by a real number is an imaginary number:

j100/50 = j2

j50/100 = j0.5

The division of a real number by an imaginary number is an imaginary number, but the negative of what would have resulted if their types were reversed:

100/j50 = -j2

50/j100 = -j0.5

-50/j100 = j0.5

Fundamentals of Guitar Amplifier System Design - design your amp using a structured, professional methodology.

A Secret for Remembering All These Rules

This all seems rather tedious, but there is a very convenient memory aid to remember these rules. We simply pretend that j is a number, specifically

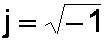
Let me clearly state that this is not actually true! j is a symbol indicating that a number is imaginary. It is not actually a number itself. Nevertheless, all of the rules we have just listed can be derived on the fly by remembering this simple expression:

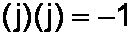
formula for the product of two imaginary numbers

We essentially use all the standard techniques of common algebra, but whenever we see a term with j² we replace it by (-1). (If you are a mathematician and consider the mere existance of j² to be a bastardization of the natural order, a lunacy of galactic proportions, a theoretical heresy for the sake of expediency, then I apologize.)