Pierre-Simon Laplace Frequency Response Plots
In working with complex impedances you frequently find yourself writing j times 2 times pi times f, over and over again. Some people like to shorten this by using radians. This leaves you with only writing j times omega. Personally, I like to carry this efficiency to the ultimate extreme by borrowing from Pierre-Simon Laplace. I use one letter to represent all four terms:
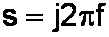
The Laplace transform is used by engineers to solve linear ordinary differential equations. It essentially transforms a complicated calculus problem into a simple algebra problem. Fortunately we don't need to know anything about the calculus that the Laplace transform represents. Instead, let's just stick with the algebra.
Laplace for Inductors
Under certain mathematical conditions which have no relevancy to the treble response of your Fender Deluxe 5E3, the impedance of an inductor, expressed in terms of Laplace, is
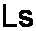
When we substitute
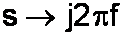
we recognize the impedance of an inductor as a function of frequency and inductance:
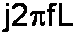
Our Laplace version is certainly shorter, but we could have chosen any letter. By sticking with s we are consistent with current usage. Show an electronic engineer the term Ls and you'll get instant recognition. Try to use Lt or Lu and you'll have some serious explaining to do. In that case don't refer your EE friends to me - you're on your own!
|
New! Guitar Amplifier Electronics: Fender Deluxe - from TV front to narrow panel to brownface to blackface Reverb |
Laplace for Capacitors
According to Laplace, a capacitor's impedance is
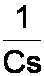
This time when we substitute
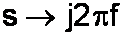
we get
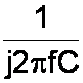
This doesn't quite look right, because j is in the denominator instead of the numerator. To get a more familiar representation, we multiply the numerator and denominator by j:
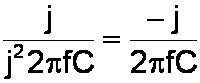
Did I really say "multiply by j?" The sound you hear is Laplace rolling over in his grave! As I said in the tutorial on imaginary numbers, j is a symbol indicating that a number is imaginary. It is not actually a number itself. But to save some extra steps and some extra mathematical jargon, this technique works for me. As Munro Saki once said, "a little approximation sometimes saves tons of explanation."
|
Guitar Amplifier Electronics: Basic Theory - master the basics of preamp, power amp, and power supply design. |
Laplace for Resistors
The Laplace transform representation of a resistor with a value of R ohms is simply, drumroll please... , R. Now that was easy!
Plotting the Frequency Response
To plot a frequency response expressed in terms of the Laplace transform, we first substitute
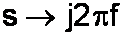
and then take the magnitude of the result. We'll see an example in the next problem.
|
Fundamentals of Guitar Amplifier System Design - design your amp using a structured, professional methodology. |
Problem
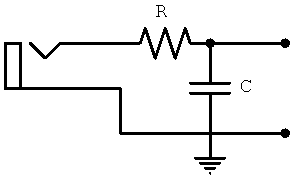
Consider again the Fender Harvard 5F10 input circuit. The resistance R and the Miller capacitance C form a voltage divider. What is the magnitude of the output voltage compared to the input voltage as a function of frequency?
Solution
The resistor and the Miller capacitance combine to form a voltage divider, where Z1 = R and Z2 = 1/Cs. The output voltage is
The frequency response is thus
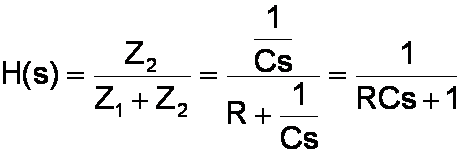
This is an extremely compact form, which is why engineers like me love it. We don't get out much. This equation is also a complete description, because it contains both magnitude and phase information, expressed by using complex values. To plot the magnitude of the frequency response, we first substitute
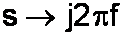
to get
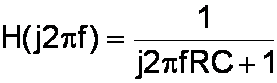
We multiply the numerator and the denominator by
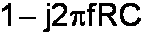
to eliminate the imaginary term in the denominator:
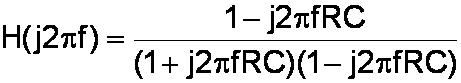
which simplifies to
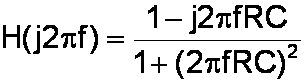
Next we separate the real and the imaginary terms:
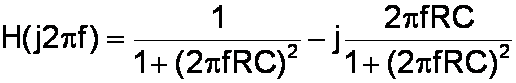
To convert the complex response to a magnitude response, we square the real and imaginary components, add them together, and take the square root of the total.
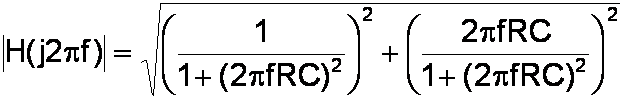
This gives us the magnitude of the frequency response:
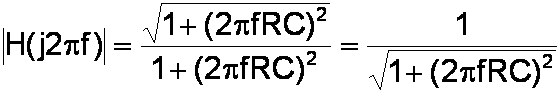
That's it! We've been using the Pierre-Simon Laplace Transform, an advanced mathematical concept that lives in the halls of Princeton, MIT, and Technical University Berlin.
The nice thing is, we don't need to know how to design a Boeing 737 to fly one to Cincinnati.
