Hiwatt CP103 Tone Stack
Here is the tone stack from the Hiwatt CP103, better known as the amp created for The Who. The stack is also found in Sound City amplifiers like the SC-105.
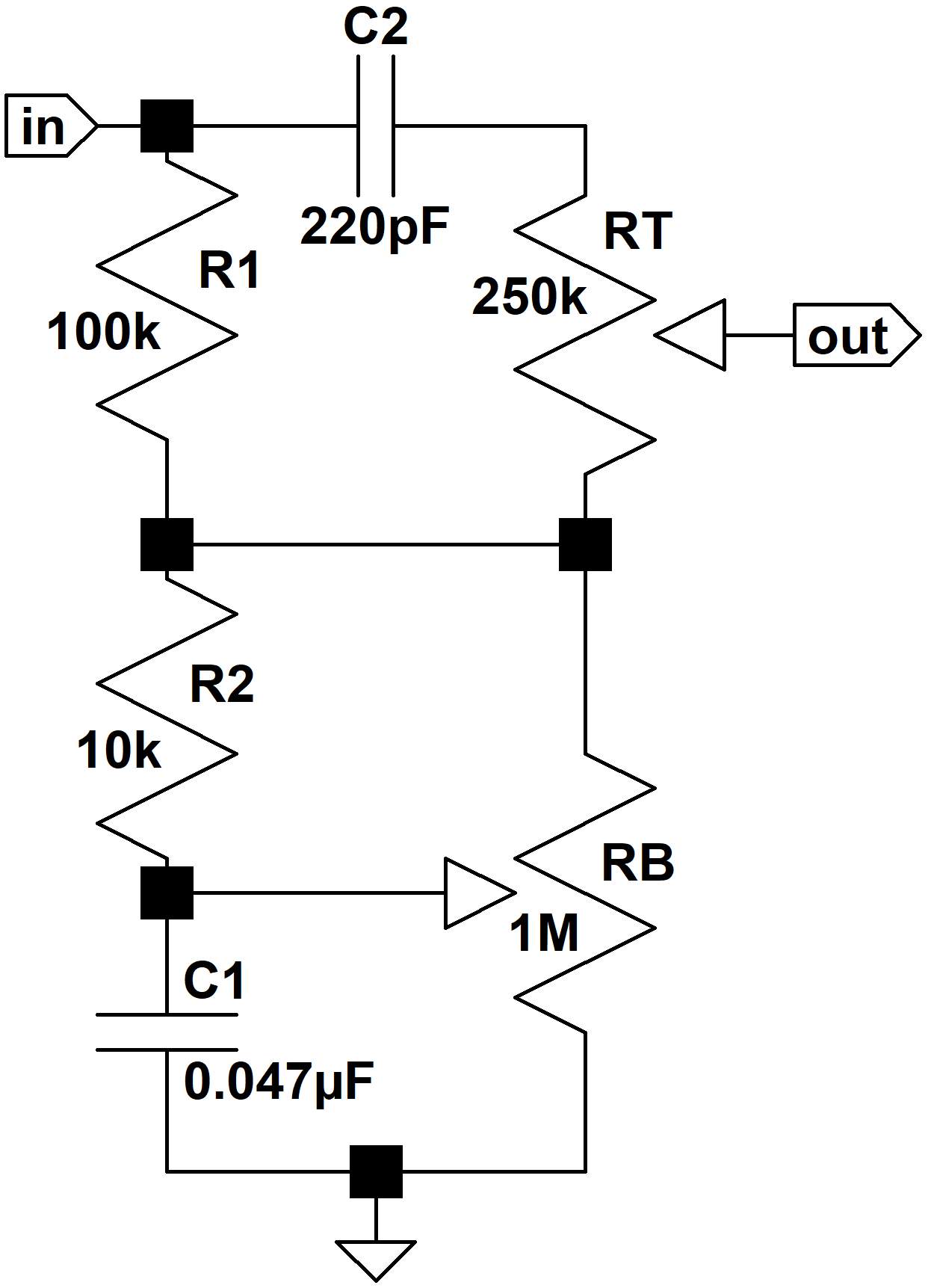
To simplify the mathematics, we'll make two important assumptions. First, we'll assume that the driving circuit has an output impedance of zero. For a low-impedance driver like a cathode follower, this is a highly-accurate assumption. The CP103's driving stage is a 12AX7 voltage amplifier with a 220k plate load resistor and a partially bypassed cathode resistor. Its output impedance is 49kΩ at treble frequencies and even higher for bass. Nevertheless this simplification will turn out to be good enough to create an accurate design.
Second, we will assume that the tone stack output drives an infinite input impedance. Tone stacks often drive a 1MΩ grid resistor. The Hiwatt uses a 250kΩ master volume control in this position, but we'll see that this simplification is also justified, because the results are very similar.
These assumptions make it easier to turn our analysis around, so that we can calculate the required parts values based on a desired frequency response. Once these parts values are finalized we can test the results under real circuit conditions.

|
Guitar Amplifier Electronics: Fender Deluxe - from TV front to narrow panel to brownface to blackface Reverb |
Maximum Bass, Minimum Treble
Let's begin by setting the bass at maximum and the treble control at minimum. This shorts R2 and connects the output directly to the bottom of RT.
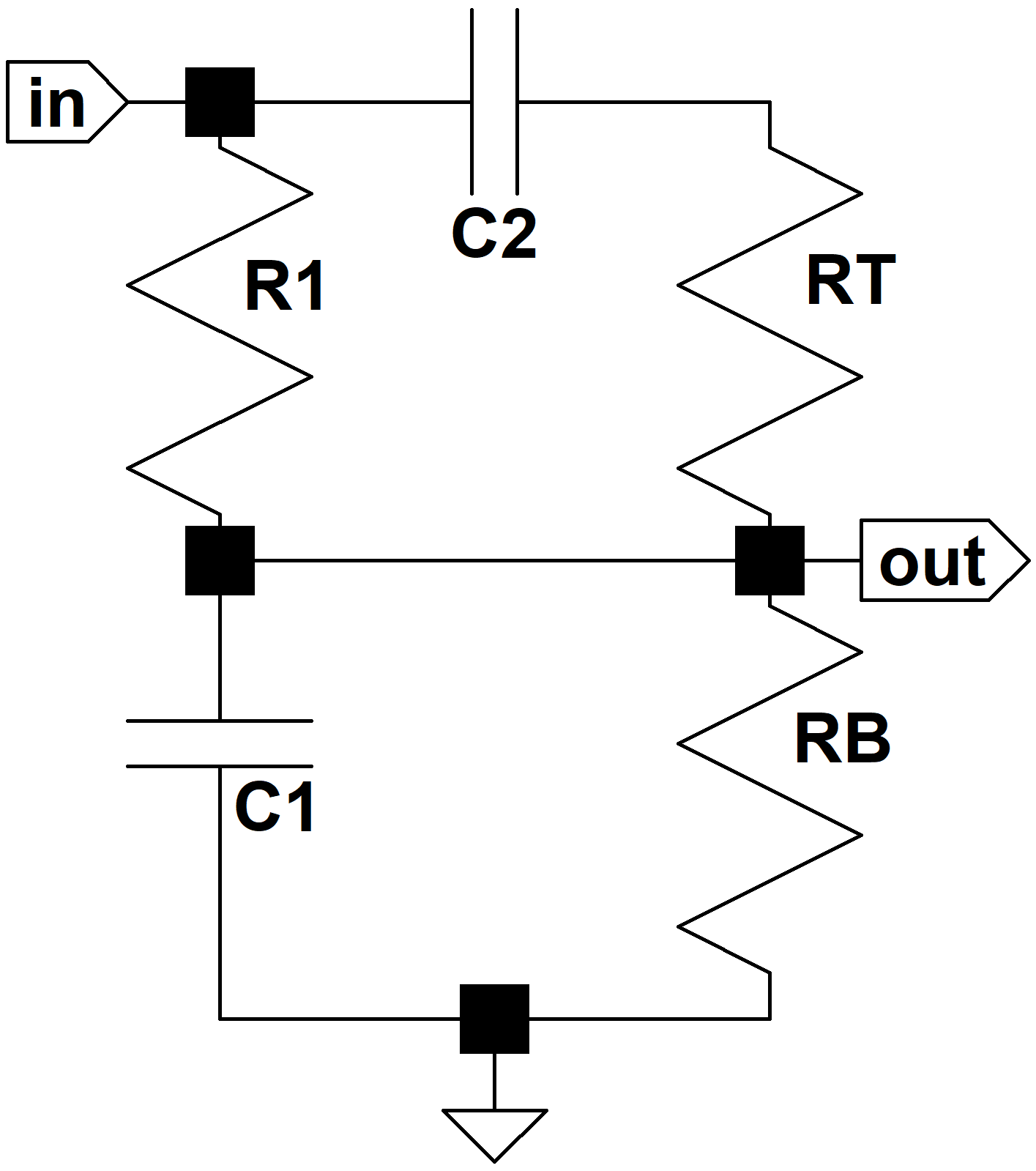
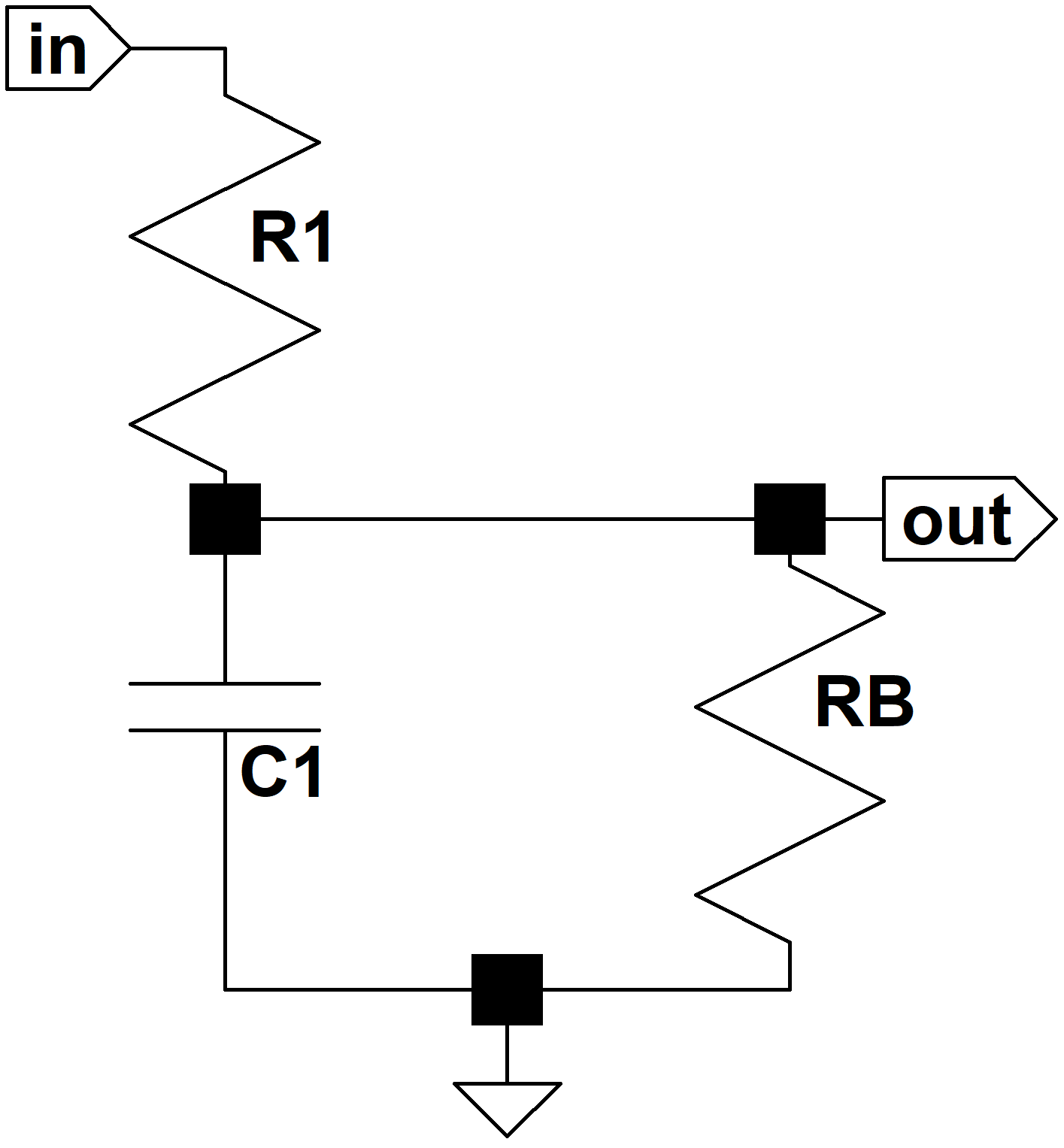
C2 is smaller than C1 and dominates performance only at treble frequencies. With the treble control at minimum it is in series with RT, which is larger than R1. For all practical purposes we can ignore C2 under these conditions.
Because we're driving an assumed open circuit, there is no current through RT and by Ohm's Law there is no voltage across it. Thus we can treat it as a short circuit, giving us a classic voltage divider where Z1 = R1 and Z2 is equal to the impedance of C1 in parallel with the bass control.
The frequency response is then
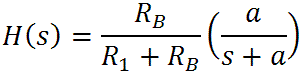
where
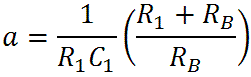
(If the variable "s" looks unfamiliar, please see our tutorial on Laplace notation.) By arranging the formula this way we can clearly see a gain of
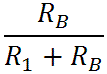
and a pole at s = -a. Let's look at the extremes of frequency. At DC, where s = 0, we get
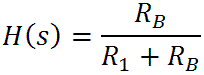
This makes sense, because C1 is open, making the circuit a simple voltage divider formed by R1 and RB. As the frequency goes to infinity the output goes to zero. This also makes sense, because C1 shorts the signal to ground.
At very low frequencies the gain is constant, as determined by the two resistor values. As the frequency rises the gain begins to decrease, falling by 3dB at the pole's transition frequency:
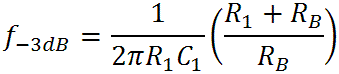
Above this frequency the response decreases at a rate of 6dB per octave (20dB per decade) until C2 begins to conduct. (As mentioned, however, C2 doesn't have much effect because of the 250kΩ resistance represented by RT. We'll clearly see this in simulation.) For the Hiwatt CP103 amplifier, where R1 = 100k, C1 = 0.047uF, and RB = 1MΩ, low-frequency gain is minus 0.8dB and the transition frequency is 37Hz.

|
Guitar Amplifier Electronics: Basic Theory - master the basics of preamp, power amp, and power supply design. |
Now we are ready to draw the Bode magnitude plot for the bass control at maximum and the treble control at minimum. We can combine the gain and the pole by drawing a horizontal line at -0.8dB until we reach the transition frequency of 37Hz. Then we draw a line sloping downward at the rate of 20dB per decade. The actual frequency response is is 3dB lower at the transition point, as shown in the plot:
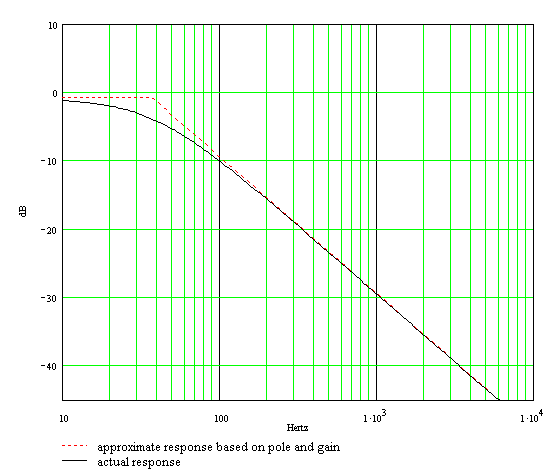
The approximate pole response and and overall gain are represented by the dotted line. The actual response, which includes the 3dB difference at the transition point, is the solid curve.
Here is the response using Electronics Workbench Multisim®. In this case the plot assumes a driving circuit output impedance of zero and a driven circuit input impedance of infinity so that we can directly compare the results.
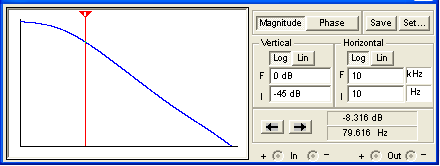
(The horizontal axis is a log scale of frequency from 10Hz to 10kHz and the vertical scale is from -45dB to 0dB.) If you look very closely you can see a very slight upturn in response due to C2 conduction at treble. Otherwise the results are identical to what we obtained assuming the capacitor was an open circuit. Here is the response when we include CP103 conditions: a 49kΩ driving impedance and a 250kΩ load.
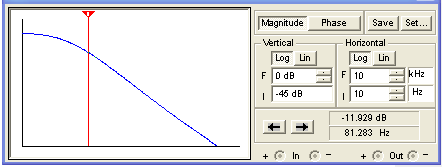
We observe additional attenuation for very low frequencies. The actual response is a bit more exaggerated by the CP103's partially bypassed cathode resistor, but not significantly. For the lowest note of a guitar with standard tuning, 82Hz, the difference between assumed and actual conditions less than 1dB.

|
Fundamentals of Guitar Amplifier System Design - design your amp using a structured, professional methodology. |
Minimum Bass, Maximum Treble
Next we reverse the control settings. With the bass control at minimum C1 is shorted and R2 is in parallel with RB. In the CP103 R2 is 100 times smaller than RB, completely dominating the effective impedance. Here is the effective circuit when the bass control is at minimum and the treble control is at maximum:
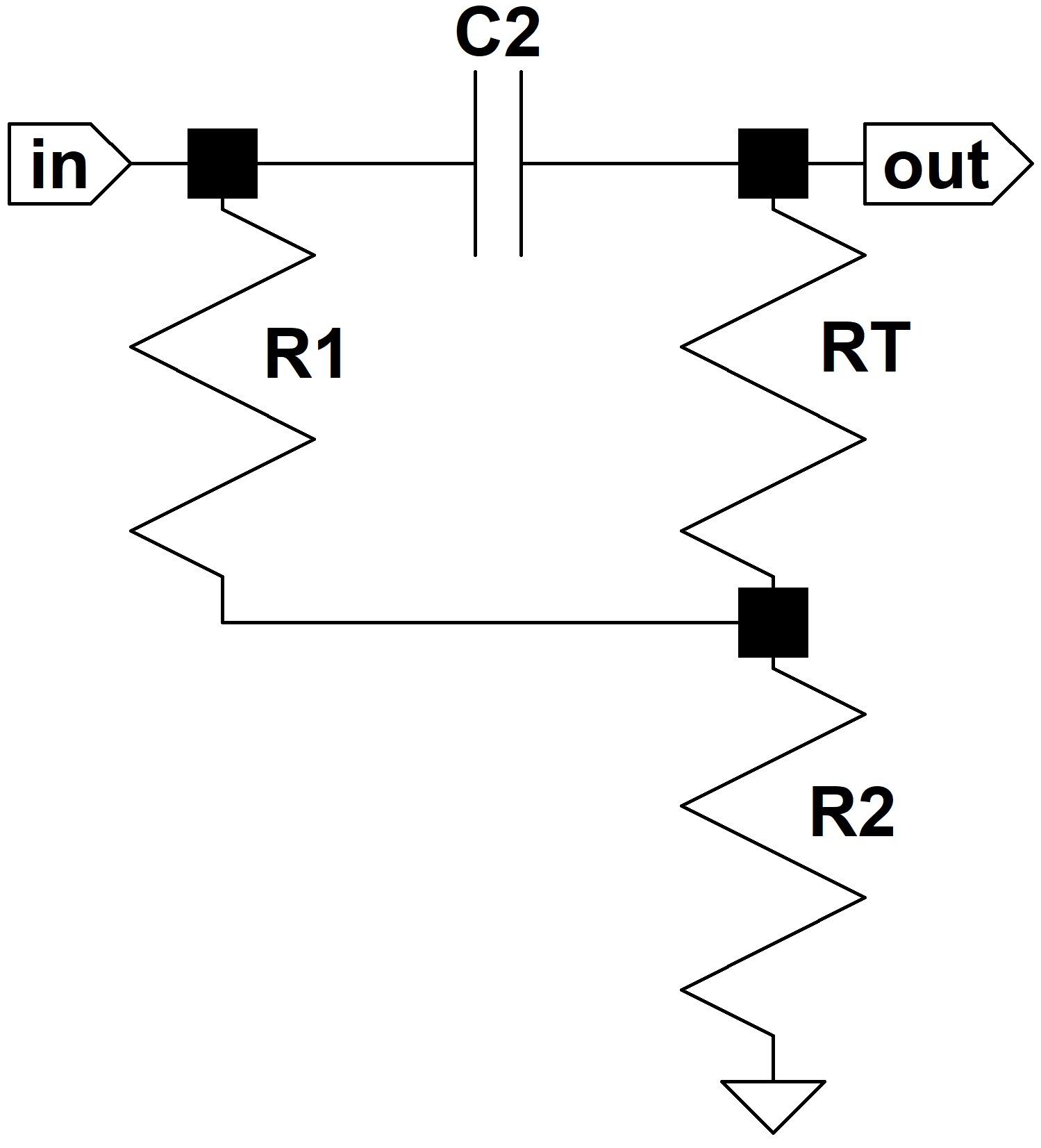
The frequency response is
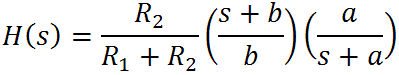
where
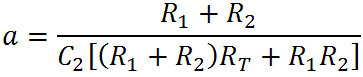
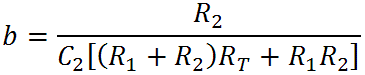
From these formulas we see that there is a gain of
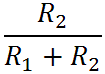
and transition frequencies for a pole at -a and a zero at -b:
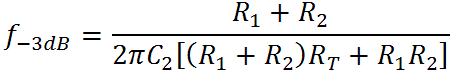
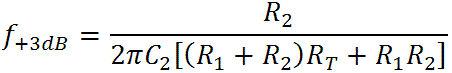
The second represents the midrange-treble transition frequency, which for CP103 component values is 254Hz. The first represents a transition to zero attenuation at 2.8kHz.
The response begins at the midrange level created by the voltage divider formed by R1 and R2. It then breaks upward due to the zero at the midrange-treble transition frequency, ultimately rising at a maximum rate of 20dB per decade. Finally it breaks back to a flat response at the second transition frequency due to the pole. Here is the Bode magnitude plot for the bass control at minimum and the treble control at maximum:
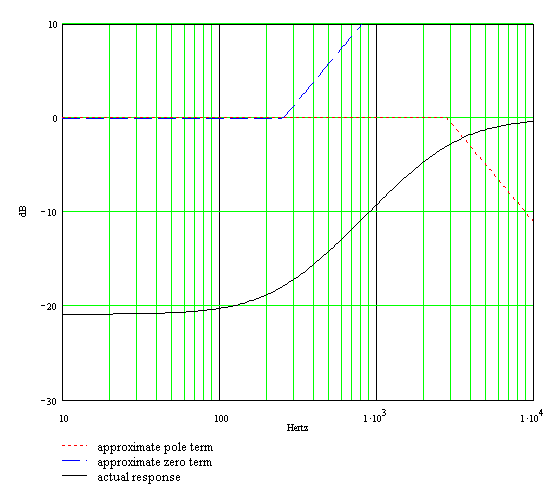
We see substantial bass cut and a transition through midrange to zero attenuation for treble.
Here is the simulated response, where the driving circuit output impedance is 49kΩ, and the driven circuit input impedance is 250kΩ:
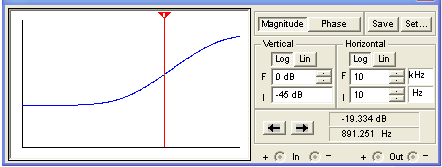
The results are almost the same, except for additional bass attenuation due to the greater-than-ideal driving impedance.

|
Guitar Amplifier Electronics: Circuit Simulation - know your design works by measuring performance at every point in the amplifier. |
Bass and Treble Controls at Minimum
When the tone controls are set to minimum we get this circuit:
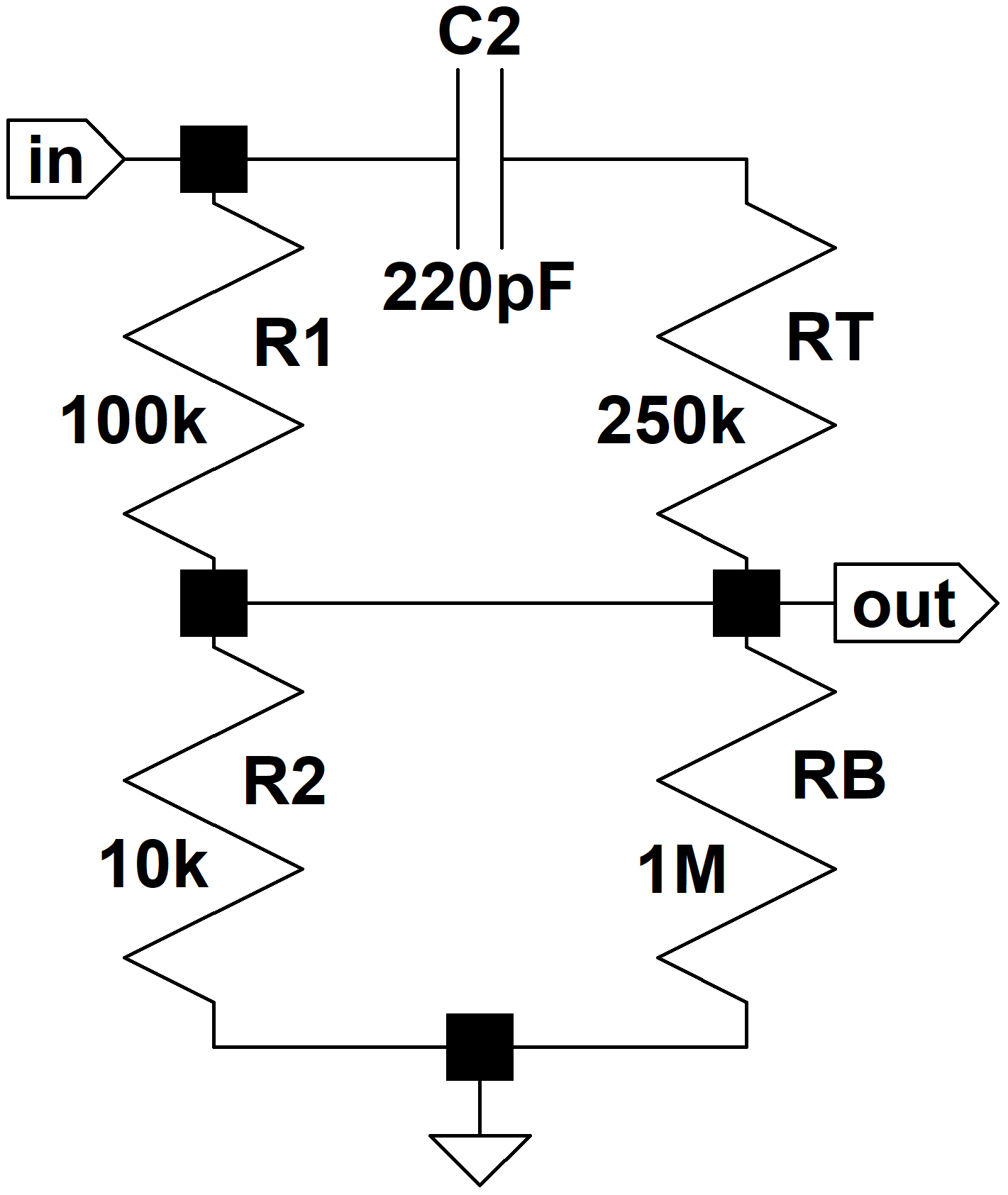
Since RB is 100 times large than R2 this is almost identical to
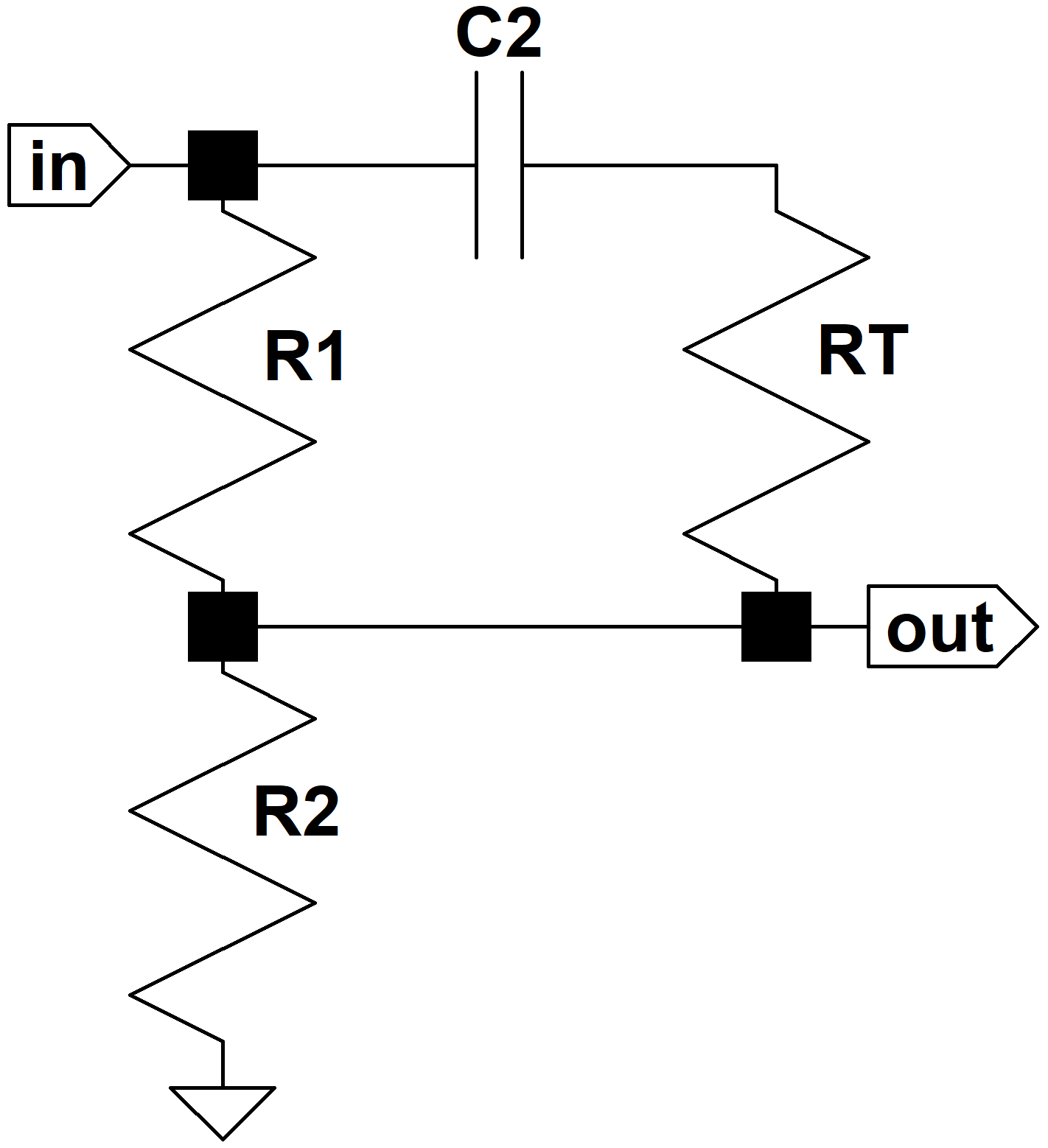
The circuit has a familiar looking frequency response:
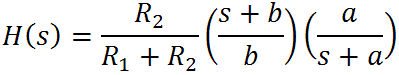
where
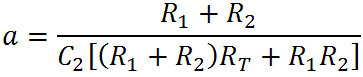
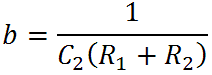
At DC, when s = 0, the gain is that same as for a voltage divider formed by R1 and R2, which for the CP103 is -21dB. This makes sense because the capacitor is an open circuit, there is no current through R2, and thus no voltage drop across it.
At extremely high frequencies the gain is

which, if we work the math, represents the same voltage divider but with R1 replaced by R1 in parallel with RT. Thus C2 is predictably acting as a short circuit. For the CP103 this is -18dB, representing treble boost of only 3dB compared to bass frequencies.
There is a pole at s = -a and a zero at s = -b. The transition frequencies for the pole and zero, respectively, are
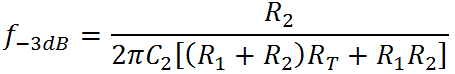
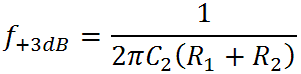
which for the CP103 are 2.8kHz and 2.1kHz. Here we see why there is only a 3dB difference between the bass and treble response: the zero and pole are fairly close together. At extremely low frequencies, the gain is -21dB. At the first transition frequency the zero kicks in and the gain starts to increase. At the second transition frequency the pole causes the gain to level back out and thereafter we get a flat response. Here is the Bode magnitude plot:
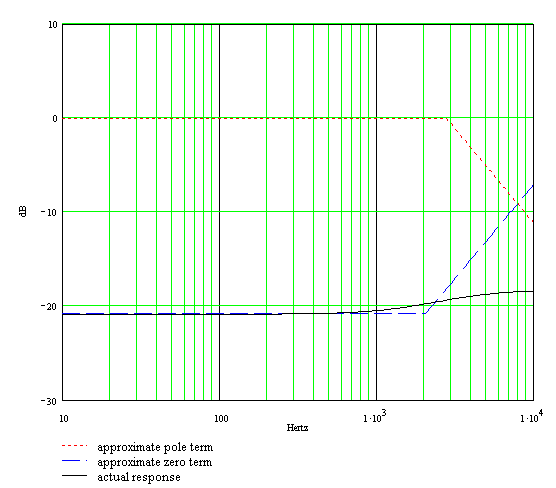
Here is the simulated response with the controls set to minimum. (The driving circuit output impedance is 49kΩ, and the driven circuit input impedance is 250kΩ.)
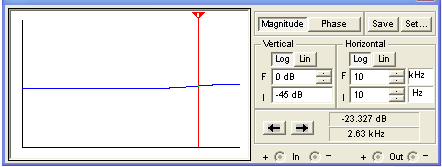
Under real circuit conditions the response is nearly identical.
Maximum Bass, Maximum Treble
The one combination we haven't examined yet is for the bass and treble controls at maximum. In this case both capacitors interact to create midrange attenuation, thereby creating the equivalent of bass and treble boost. We could compute this response directly by applying Kirchoff's Voltage Law over multiple loops, but having already looked at bass and treble boost in isolation, this is hardly necessary.
The complete response combines the two responses we studied previously. The bass transition for the CP103 was at 37Hz when the bass control was at maximum and the treble control was at minimum. When we reversed the tone control positions we observed a treble transition of 2.8kHz. Having both tone controls at maximum brings these two conditions together, creating midrange scoop roughly centered between 37Hz and 2.8kHz on a logarithmic scale. Taking the log of each frequency, adding them, dividing the result by two and then taking the inverse log gives us 322Hz. A more easily obtained estimation is to look at the bode plots and pick the frequency about halfway between. Either way the results are very close, as this simulation shows:
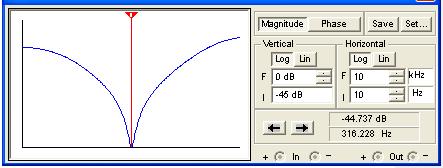
The plot incorporates a driving circuit output impedance of 49k and a driven circuit input impedance of 250kΩ. Midrange scoop is centered around 316Hz.
Translating Theory into a Practical Design Strategy
To convert our analysis into a practical design procedure we need to translate the equations that determine the frequency response based on parts values into equations that determine parts values based on the desired frequency response. We take that step and put the formulas to practical use here:
Create Your Own Design
To convert our theoretical knowledge into a practical strategy we translate the equations that determine frequency response based on parts values into equations that determine parts values based on the desired frequency response. This will be demonstrated using a concrete example: giving the CP103 a more Bassman-like midrange scoop. Here is the simulated response of the Fender Bassman 5F6-A tone stack with its bass control at maximum, its midrange control at minimum, and its treble control at maximum:

It has a bass transition frequency of 142Hz and a treble transition frequency of 2.5kHz. Let's modify the CP103 tone stack to use these transition frequencies. A rough approximation of the expected response (with bass and treble controls at maximum) can be seen by drawing two lines. The blue line below shows a modified CP103 bass response that starts at 142Hz, 0dB, and ends one decade higher (1.42kHz) at -20dB. This represents 20dB-per-decade attenuation that begins at 142Hz.
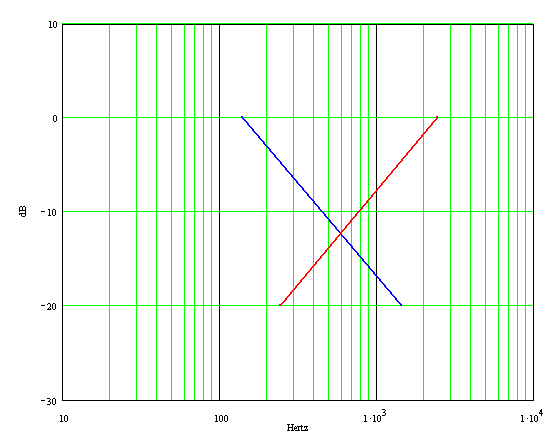
Likewise the red line shows a treble-to-midrange attenuation of 20dB per decade that begins at 2.5kHz and ends at 250Hz. (Nothing really "ends" there - it's just a convenient reference point to give the line the correct slope.) From the intersection of the blue and red lines we observe midrange scoop centered around 600Hz. Let's determine the CP103 component values needed to produce this result.
From our analysis of the CP103 tone stack the bass transition frequency is
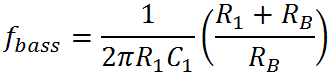
and the treble transition frequency is
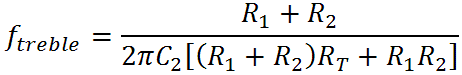
These two equations represent two constraints, and since there are many more parts values than constraints it appears we have a lot of freedom of choice. There are other factors to consider, however. The overall circuit impedance needs to be high enough not to load down the driving circuit and low enough not to be loaded down by the stage it drives. We'll therefore keep the CP103's R1 value at 100k. Out of convenience, we'll also retain the CP103 tone control values of RB = 1MΩ and RT = 250kΩ.
Another consideration is the midrange-treble transition frequency:
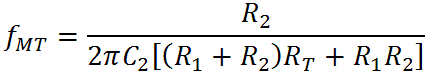
For effective tone control performance this need to be below the midrange scoop frequency. The CP103 uses a midrange-treble transition of 254Hz for a scoop frequency of 316Hz and a treble transition frequency of 2.8kHz. From the equations above this means the ratio
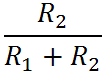
is equal to fMT/ftreble, where fMT is the midrange-treble transition frequency and ftreble is the treble-transition frequency. We can turn this concept into a design formula with just a little algebra:
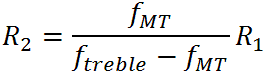
For our design, let's set fMT = 400Hz for a scoop frequency of 600Hz and set ftreble = 2.5kHz. From the formula R2 is 19k. (We'll use the more common value of 20k.)
Everything is now known except for the capacitor values, which we can determine by turning around the formulas for the bass and treble transition frequencies:
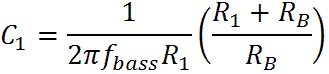
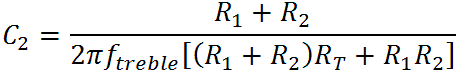
For our desired transitions at 142Hz and 2.5kHz we get C1 = 0.012uF and C2 = 240pF. Here are the final results:
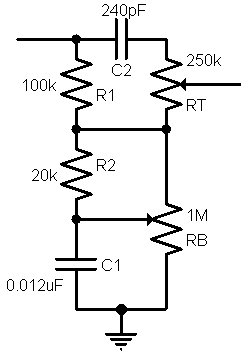
Simulating the Results
Here is the response using Electronics Workbench Multisim®. This plot assumes ideal conditions: zero source impedance and an infinite-impedance driven stage. These were the conditions we used to determine the parts values.
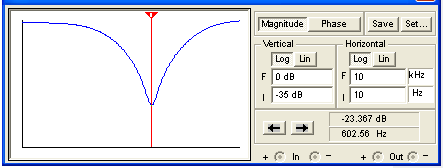
(The horizontal axis is a log scale of frequency from 10Hz to 10kHz and the vertical scale is from -35dB to 0dB.) Here is the same plot using CP103 operating conditions: a driving circuit output impedance of 49kΩ and a driven circuit consisting of a 250kΩ volume control.
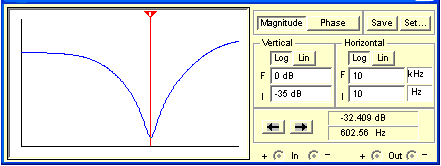
For the same conditions, here is the response with the bass control at maximum and the treble control at minimum:
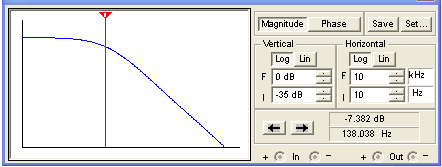
Bass control at minimum and treble control at maximum:
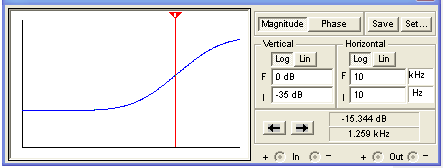
Both controls at minimum:

|
From system design concepts to individual stage operation, an all-new examination of Bassman electronics. |


