TUTORIAL - PENTODE PREAMP DESIGN
Part 3 - AC Operating Conditions
Here is our design so far.
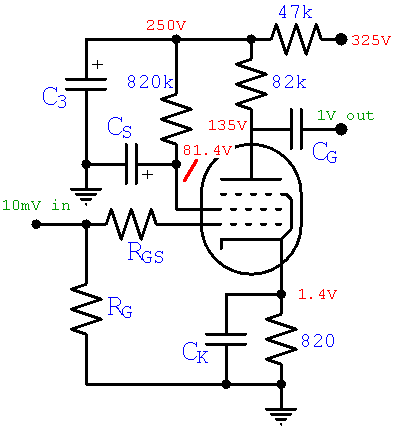
To eliminate negative feedback from cathode degeneration,1 the bypass capacitor CK needs to be large enough to short all audio frequencies. The required value depends on the cathode impedance ZK, which is equal to the 820Ω cathode resistor RK in parallel with the reciprocal of the tube's transconductance gm that we estimated earlier:
ZK = 820Ω || [1 / (1.5ma/V)] = 368Ω
The lowest note on a guitar with standard tuning is 82 Hertz. So if we select a capacitor whose impedance is equal to the cathode impedance at a frequency 10 times lower, 8.2 Hertz, then we can be fairly certain that we've eliminated negative feedback:
CK = 1 / [2π(8.2Hz)(368Ω)] = 53μF
A 50μF value will suffice. Let's pull a similar trick to solve for the screen capacitor CS.
|
New! Guitar Amplifier Electronics: Fender Deluxe - from TV front to narrow panel to brownface to blackface Reverb |
A pentode has screen resistance rs that is analogous to the plate resistance rp in a triode. Since the ratio of plate current to screen current is about 6 to 1, the screen resistance rs is about 6 times greater than the plate resistance when the tube is triode-connected. Here are the triode-connected plate characteristics:
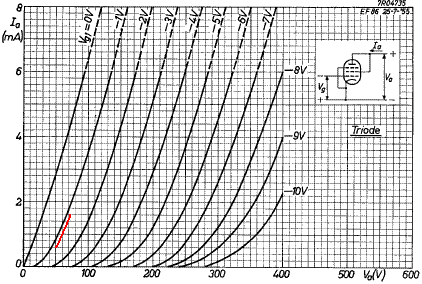
From the red line in the vicinity of the DC operating point, we observe that the plate voltage increases 22 volts when the plate current increases 1 milliamp. According to Ohm's Law this represents a plate resistance of 22kΩ, so screen resistance is about 6 times greater: 132kΩ. To make the impedance of the screen bypass capacitor CS equal to 132kΩ at a tenth the lowest frequency of a guitar, the capacitor value is
CS = 1 / [2π(8.2Hz)(132kΩ)] = 0.15μF
|
Guitar Amplifier Electronics: Basic Theory - master the basics of preamp, power amp, and power supply design. |
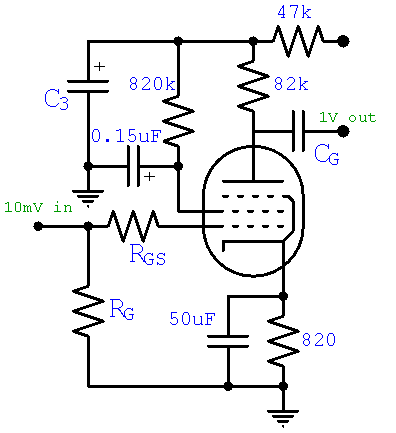
The Grid Circuit
The EF86 has about 5 picofarads of capacitance between the grid and cathode and only 0.05pF between the grid and plate. Because of the Miller Effect,2 the capacitance between the grid and plate is multiplied by 1 plus the stage gain of 100, so the total Miller capacitance is
CM = 5pF + (1 + 100)(0.05pF) = 10pF
A 12AX7 has ten times more parasitic capacitance, which is bad news for radio and why you won't find Marshall's favorite triode in the front end of a Philco. To ensure that radio-frequency suppression in our EF86 preamp begins at a cutoff frequency of 100kHz, the grid stopper resistor value needs to be
RGS = 1 / [2π(100kHz)(10pF)] = 159kΩ
We will use 150kΩ. A grid resistor value of RG = 1MΩ is a standard that places only a light load on the guitar circuit while providing sufficient grid leak.
|
Fundamentals of Guitar Amplifier System Design - design your amp using a structured, professional methodology. |
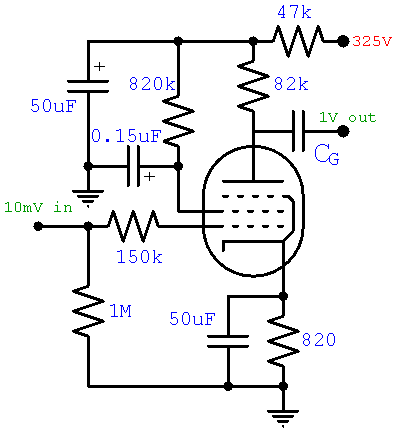
As a final order of business, power supply filter capactor C3 needs to be large enough to mitigate AC ripple and decouple the preamp from later stages.3 The specific value depends on the rest of the amp. Since R3 is a respectable 47kΩ, setting C3 to 50μF creates an impressive 65dB of ripple suppression, as shown by this snapshot of our RC Ripple Filter calculator.
Here is the final design.
References
1Richard Kuehnel, Guitar Amplifier Electronics: Basic Theory, (Seattle: Amp Books, 2018), p. 61.
2Richard Kuehnel, Guitar Amplifier Electronics: Basic Theory, (Seattle: Amp Books, 2018), pp. 70-72.
3Richard Kuehnel, Fundamentals of Guitar Amplifier System Design, (Seattle: Amp Books, 2019), pp. 100-113.
